Distributor pipe

Analytical relationship for the direct calculation of pressure drops in pipes distributing a flow rate in a homogeneous manner based on the Blasius formula.

Assumptions

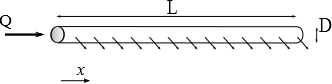
We assume a pipe length $L$, inner diameter $D$, with a flow rate at the top $Q$. We calculate the pressure drop between the two ends of the pipe. In a constant flow section $q$, the friction coefficient is evaluated with the Blasius formula, valid for moderate Reynolds numbers for smooth walls:

$$\lambda \simeq aR{e}^{-0.25}$$

Analytical development

We're recording the position from the downstream end of the pipe. The flow rate is supposed to vary linearly with $x$, and is then written:

$$q(x)=Qx/L$$

Let's note $S=\pi D^2/4$ the inner surface of the pipe. The pressure drop is obtained by integrating the Darcy-Weisbach relationship:

$$\mathrm{\Delta }H={\int }_{x=0}^{L}aR{e}^{-0.25}\frac{u^2(x)}{2gD}dx$$

Note the kinematic viscosity. We then replace $Re$ with $uD/\nu$, which gives

$$\mathrm{\Delta }H={\int }_{x=0}^{L}au(x{)}^{-0.25}{D}^{-0.25}{\nu }^{0.25}\frac{u^2(x)}{2gD}dx$$

By rearranging, we get:

$$\mathrm{\Delta }H={\int }_{x=0}^{L}a{\nu }^{0.25}\frac{u^{1.75}(x)}{2g{D}^{1.25}}dx$$

Let's use the flow equation to show the flow ($u(x)=q(x)/S$):

$$\mathrm{\Delta }H={\int }_{x=0}^{L}a{\nu }^{0.25}\frac{(Qx/(LS){)}^{1.75}}{2g{D}^{1.25}}dx$$

then the diameter:

\($\mathrm{\Delta }H={\int }_{x=0}^{L}a{\nu }^{0.25}\frac{(4Qx/(L\pi D^2){)}^{1.75}}{2g{D}^{1.25}}dx$\) We rearrange to get

$$\mathrm{\Delta }H=a{\nu }^{0.25}\frac{(4/\pi {)}^{1.75}{Q}^{1.75}}{2g{D}^{4.75}}{\int }_{x=0}^L(x/L{)}^{1.75}dx$$

By integrating, we obtain

$$\mathrm{\Delta }H=a{\nu }^{0.25}\frac{(4/\pi {)}^{1.75}{Q}^{1.75}}{2g{D}^{4.75}}\frac{L}{2.75}$$

$$\mathrm{\Delta }H=a{\nu }^{0.25}\frac{4^{1.75}}{5.5g{\pi }^{1.75}}{Q}^{1.75}L{D}^{4.75}$$

Digital application

For water at 20°C: $\nu \simeq {10}^{-6}$ m²/s, which gives

$$DeltaH=0.323{10}^{-3}\frac{Q^{1.75}}{D^{4.75}}L$$

with $\mathrm{\Delta }H$ in meters.

For water at 50°C, $\nu \simeq 0.556{10}^{-6}$ m²/s, which means that the pressure drop is reduced by about 14%, or

$$DeltaH=0.28{10}^{-3}\frac{Q^{1.75}}{D^{4.75}}L$$