"Fatou" baffle fiwhway
Geometrical characteristics
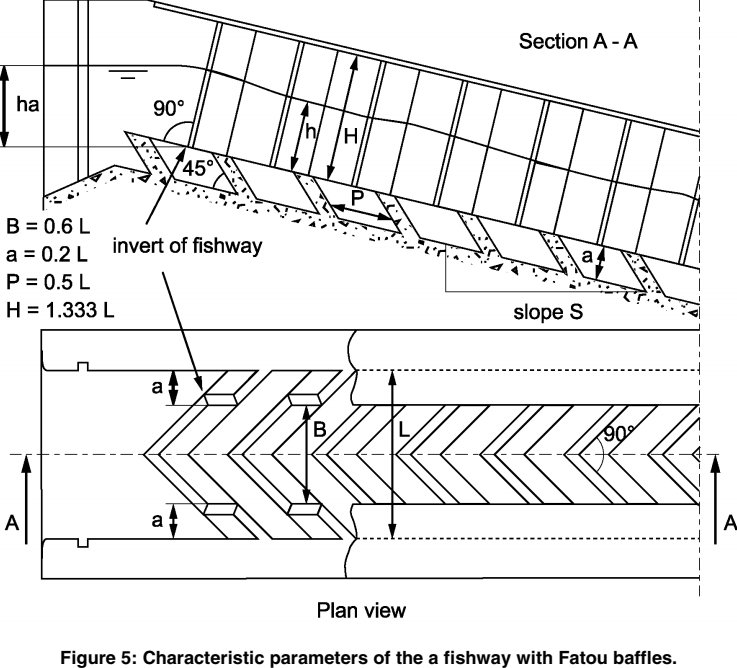
Excerpt fromLarinier, 20021
Hydraulic laws given by abacuses
Experiments conducted by Larinier, 20021 allowed to establish abacuses that link adimensional flow
to upstream head
Abacuses of a Fatou baffle fishway for a slope of 10% (Excerpt fromLarinier, 20021)
Abacuses of a Fatou baffle fishway for a slope of 15% (Excerpt fromLarinier, 20021)
Abacuses of a Fatou baffle fishway for a slope of 20% (Excerpt fromLarinier, 20021)
To run calculations for all slopes between 8% and 22%, polynomes coefficients of abacuses above are themelves adjusted in the form of slope
We thus have:
And:
Calculation of
We can then use those coefficients to calculate
Using the positive inverse function, depending on
And we finally have:
Calculation limitations of
Flow velocity
Flow velocity
for Fatou baffle fishways using the notation of the schema above, we have:
Which gives with standard proportions: