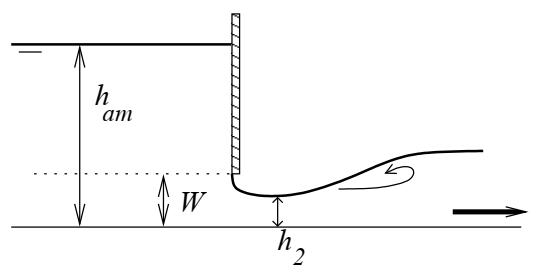
Free flow gate

Excerpt from Baume, J.-P., Belaud, G., Vion, P.-Y., 2013. Hydraulique pour le génie rural, Formations de Master, Mastère Spécialisé, Ingénieur agronome. UMR G-EAU, Irstea, SupAgro Montpellier.

\(W\) is the gate opening, \(h_{am}\) the upstream water level and \(L\) the date width. The dewatered valve equation is derived from Bernoulli's load conservation relationship between the upstream side of the valve and the contracted section.

The height \(h_2\) corresponds to the contracted section and is equal to \(C_c W\) where \(C_c\) is the contraction coefficient. The free flow gate equation is often expressed as a function of a flow coefficient in the form of:

\(Q = C_d L W \sqrt{2g} \sqrt{h_{am}}\)

So we have the relationship between \(C_d\) and \(C_c\) :

\(C_d = \frac{C_c}{\sqrt{1 + C_c W / h_{am}}}\)

Numerous experiments were conducted to evaluate \(C_d\), which varies little around 0.6. As a first approximation, for a low \(W / h_{am}\) (undershot gate, most frequent case), \(C_d\) is close to \(C_c\) and can be chosen equal to 0.6.

Discharge coefficients \(C_d\) are given by abacuses, which can be found in specialized books if necessary. They range from 0.5 to 0.6 for a vertical gate, from 0.6 to 0.7 for a radial gate, up to 0.8 for a gate inclined with respect to the vertical.