Distributor pipe
Analytical relationship for the direct calculation of pressure drops in pipes distributing a flow rate in a homogeneous manner based on the Blasius formula.
Assumptions
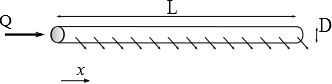
We assume a pipe length \(L\), inner diameter \(D\), with a flow rate at the top \(Q\). We calculate the pressure drop between the two ends of the pipe. In a constant flow section \(q\), the friction coefficient is evaluated with the Blasius formula, valid for moderate Reynolds numbers for smooth walls:
Analytical development
We're recording the position from the downstream end of the pipe. The flow rate is supposed to vary linearly with \(x\), and is then written:
Let's note \(S=\pi D^2/4\) the inner surface of the pipe. The pressure drop is obtained by integrating the Darcy-Weisbach relationship:
Note the kinematic viscosity. We then replace \(Re\) with \(u D/\nu\), which gives
By rearranging, we get:
Let's use the flow equation to show the flow (\(u(x)=q(x)/S\)):
then the diameter:
\(\(\Delta H=\int_{x=0}^{L} a \nu ^{0.25} \frac{(4Qx/(L\pi D^2))^{1.75}}{2gD^{1.25}}dx\)\) We rearrange to get
By integrating, we obtain
Digital application
For water at 20°C: \(\nu\simeq 10^{-6}\) m2/s, which gives
with \(\Delta H\) in meters.
For water at 50°C, \(\nu\simeq 0.556 10^{-6}\) m2/s, which means that the pressure drop is reduced by about 14%, or