Kindsvater-Carter and Villemonte formula

The calculation module allows hydraulic calculations to be carried out for several structures in parallel.

Kindsvater-Carter formula (1957)

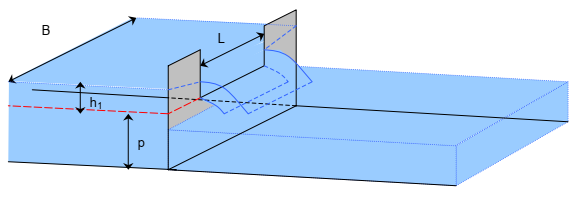
Figure 12: perspective view of a rectangular weir with lateral contraction.

Kindsvater-Carter formula corresponds to the classic weir formula:

\[Q = \mu L \sqrt{2g}h_1^{1.5}\]

With:

• \(\mu\) the discharge coefficient \(\mu = \alpha + \beta h_1/p\)
• \(L\) the width of the weir
• \(h_1\) the water level above the weir crest
• \(p\) the sill or weir crest height

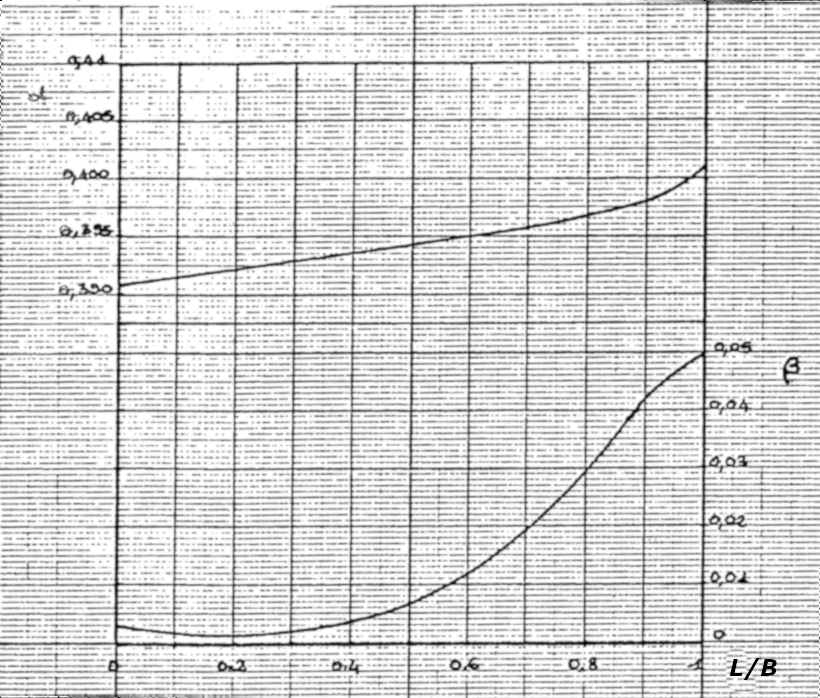
The coefficients \(\alpha\) and \(\beta\) depend on the ratio between the width of the weir (\(L\)) and the width of the basin (\(B\)). Their values are given in the abacuses below (Excerpt from Larinier, M., Porcher, J.-P., 1986. Programmes de calcul sur HP86 : hydraulique et passes à poissons):

Submerged flow: Villemonte formula (1947)

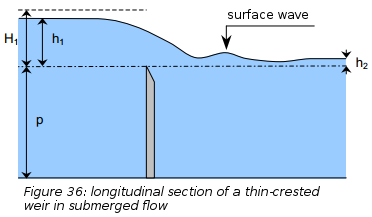
For a downstream water elevation higher than the elevation of the weir crest, the flow is submerged and a flooding coefficient is applied to the flow coefficient.

Villemonte proposes the following formula:

\[K = \frac{Q_{submerged}}{Q_{free}} = \left [ 1- \left ( \frac{h2}{h1} \right)^n \right]^{0.385}\]

With: - \(h_1\) the upstream water level above the weir crest - \(h_2\) the downstream water level above the weir crest - \(n\) the exponent in free flow relationships (rectangular=1.5, triangular=2.5, parabolic=2)