Skip to content

V-notch weir formula

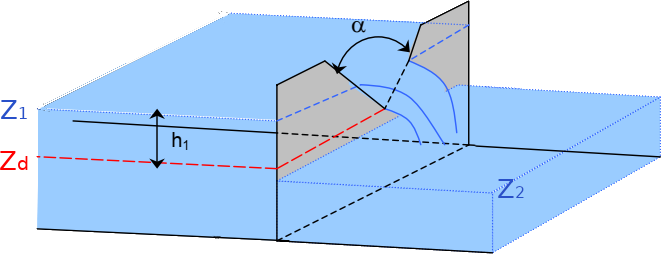
Perspective view of a triangular weir

Perspective view of a triangular weir (from CETMEF, 20051)

Free flow formula

\[Q = C_d * \tan \left( \frac{\alpha}{2} \right) \left ( Z_{1} - Z_d \right )^{2.5}\]

Avec:

  • \(C_d\) : discharge coefficient
  • \(\alpha / 2\) : half-angle at the apex of the triangle
  • \(Z_1\) : upstream water elevation
  • \(Z_d\) : spill elevation at the tip of the triangle

The discharge coefficient \(C_d\) depends, among other things, on the thickness of the weir:

  • Sharp-crested weir : \(C_d\) = 1.37
  • Broad-crested weir (rounded off \(r > 0.1 * h1\)) : \(C_d\) = 1.27
  • triangular profile weir : (1/2 upstream, 1/2 or 1/5 downstream) : \(C_d\) = 1.68 and 1.56

Submergence of a V-notch sharp-crested weir

The weir is submerged as soon as \(Z_{2} > Z_{d}\) and the Villemonte reduction coefficient is then applied to the discharge calculated in free flow.

Submergence of a V-notch broad-crested weir

Submergence occurs for \(h_2 / h_1 > 4 / 5\) with \(h_1 = Z_1 - Z_d\) and \(h_2 = Z_2 - Z_d\), and with \(Z_2\) the downstream water elevation.

The reduction coefficient proposed by Bos (1989) 2 is then applied:

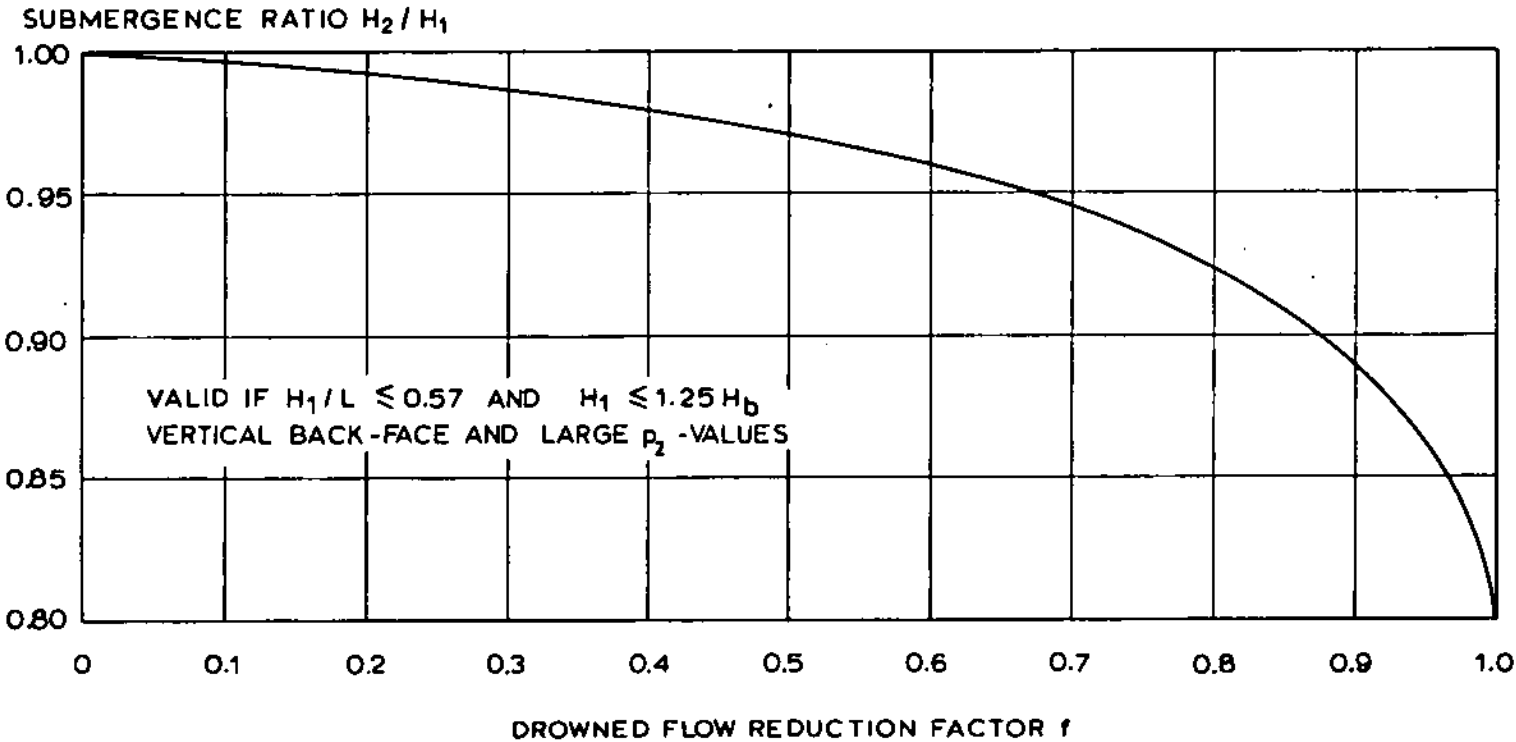
Submergence reduction factor for a V-notch broad-crested weir (from Bos, 1989 2)

Submergence reduction factor for a V-notch broad-crested weir (from Bos, 1989 2)

The abacus is approximated by the following formula:

\[K_s = sin(3.9629 (1 - h_2 / h_1)^{0.575})\]

  1. CETMEF, 2005. Notice sur les déversoirs : synthèse des lois d’écoulement au droit des seuils et déversoirs. Centre d’Études Techniques Maritimes Et Fluviales, Compiègne. ↩

  2. Bos, M.G., 1989. Discharge measurement structures., 3rd edition. ed, Publication. International Institute for Land Reclamation and Improvement, Wageningen, The Netherlands. ↩↩↩